Application of Altair OptiStruct™ in Random Vibration Analysis of Electric Bicycle Battery Module
作者:新加坡商兆普科技有限公司台灣分公司 陳信宏 副 理
新加坡商兆普科技有限公司台灣分公司 鍾維哲 資深工程師
Background
With the rapid advancement of technology, transportation and industrial vehicles are undergoing electrification, and bicycles are no exception. This study focuses on a battery pack designed for use in electric bicycles. When the battery pack is mounted on the bicycle, it experiences various road-induced load conditions during riding, which may cause structural damage to the battery pack.
If vibration-induced damage can be considered during the early stages of product design — even before development begins — the overall R&D cost can be significantly reduced.
Solution
Based on the Power Spectral Density(PSD)load conditions provided by a bicycle manufacturer, this study conducts a random vibration analysis on the battery pack using Altair OptiStruct™ to address the product’s failure behavior.
Finite Element Model Setup
In the meshing process, most of the battery pack components are made of plastic and aluminum materials. Therefore, first-order tetrahedral elements(Tetra4: CTETRA)were used for meshing. The rail is relatively thin, a refined mesh with second-order tetrahedral elements(Tetra10: CTETRA)was applied to improve local accuracy, as shown in Figure 1.

Figure 1. Exploded view of the meshed model
Initial and Boundary Condition Setup
Based on the test fixture configuration(as illustrated in Figure 2)and the input waveform from the test machine, corresponding analysis settings were applied to the simulation model. The boundary condition setup is shown in Figure 3, and the excitation load configuration is shown in Figure 4.
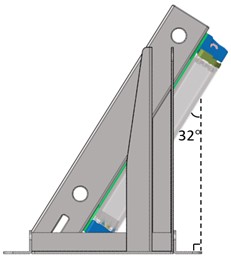
Figure 2. Test fixture setup schematic

Figure 3. Boundary condition
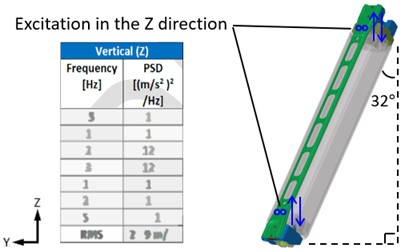
Figure 4. Excitation load setup
Analysis Results
The analysis in this study consists of two main stages: benchmark correlation analysis and structural optimization analysis. The correlation analysis was first conducted to validate the accuracy of the simulation model, followed by the optimization analysis focusing on structural improvement.
Correlation Analysis
The random vibration results were obtained and compared with the experimental data. The comparison confirmed that the high-stress regions of the baseline rail in the 3σ-RMS stress distribution corresponded to the actual failure locations observed in the vibration test, as shown in Figures 5 and 6. After verifying the accuracy of the analysis model, structural optimization was subsequently carried out.
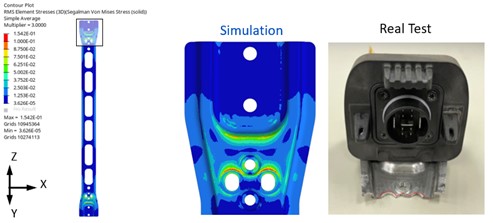
Figure 5. Comparison of upper rail: simulation vs. test
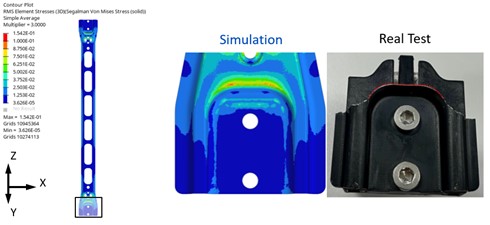
Figure 6. Comparison of lower rail: simulation vs. test
Optimization Analysis
By examining the modal shapes and frequency response results, design countermeasures were implemented on the rail structure. The modification involved reinforcing the fracture-prone region of the rail and adjusting its vibration mode to reduce resonance effects, as shown in Figure 7.
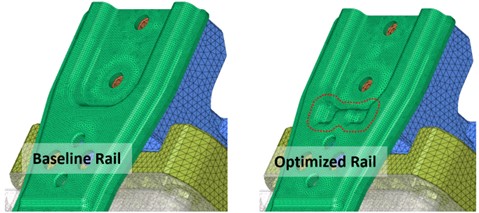
Figure 7. Rail structure countermeasures
After implementing the countermeasures, a re-analysis of the optimized rail was then performed, and the random vibration results were compared with those of the baseline rail. The results show that the optimized design exhibited a significant reduction in stress due to improved mode shapes and enhanced local stiffness. The stress distribution is illustrated in Figure 8. As summarized in Table 1, the rail stress was reduced by 12.2% to 27.9%, demonstrating the effectiveness of the optimization.
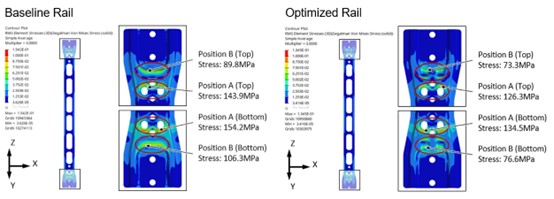
Figure 8. Comparison of rail stress distribution
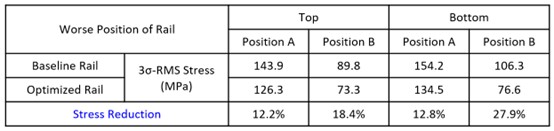
Table 1. Rail stress optimization results
Conclusion and Future Work
Through repeated adjustments of the analysis model—such as mesh refinement, simulation parameters, boundary conditions, and constraints—the correlation with experimental results was improved, making the simulation model both reliable and predictive. Based on this validated model, structural optimization was successfully performed, effectively resolving the rail fracture issue caused by random vibration.
In any finite element analysis software, it is challenging to accurately simulate vibration-related behaviors involving contact and collision between components. In this model, several parts are constrained through geometric locking structures, which cannot be fully represented in the simulation. These geometric boundary constraints may increase structural instability during vibration testing. Therefore, the assumptions for boundary conditions still require refinement based on accumulated analytical experience to achieve more realistic representations.












