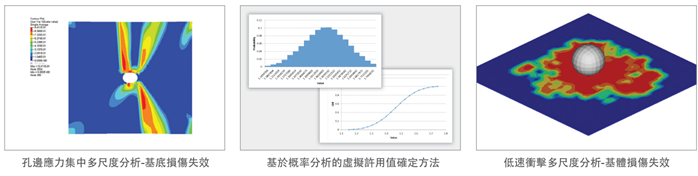
Multiscale Designer
.......Altair Multiscale Designer是一款用於開發各種多尺度材料模型並進行模擬的高效工具,適用於連續纖維、織物、短切纖維複合材料、蜂窩芯材、鋼筋混凝土、土壤、骨體
以及其他各類各向異性材料。
.......應用包括針對設計多尺度材料建模、極限失效、基於統計的材料許用強度、疲勞、斷裂、衝擊、碰撞、環境降解以及多物理場模擬,並為商用FEA求解器Altair OptiStruct、Altair Radioss、LS-DYNA和Abaqus提供外掛程式。
【 產品亮點 】
- 適用於連續、長、短纖維增強複合材料
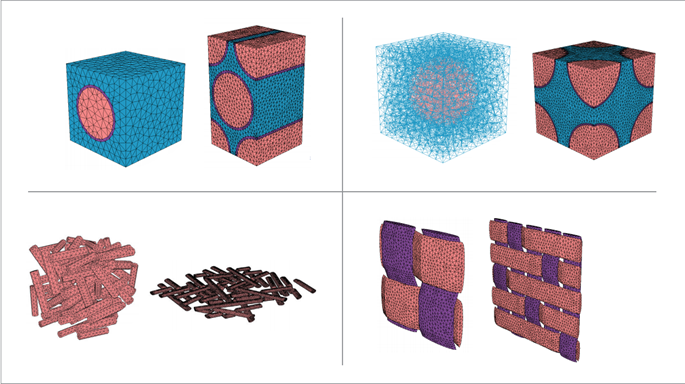
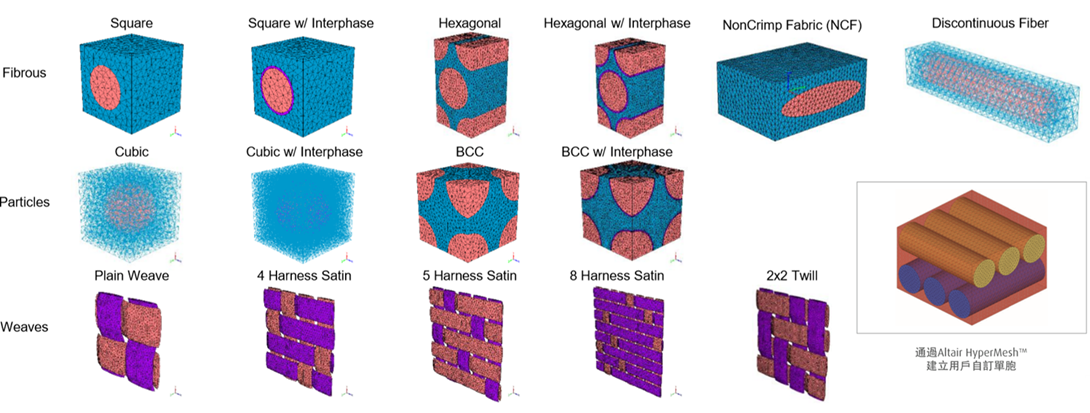
- 內建參數化單胞模型,支援使用者自訂單胞模型
- 準確、高效的模擬,材料非線性段至極限失效
- 可將模流分析的纖維流向映射到結構網格
- 內建標準實驗模型,可對材料進行虛擬實驗模擬
- 提供高效的商業有限元素求解器介面,支援Altair OptiStruct、Altair Radioss、LS-DYNA以及 Abaqus
【 優勢 】
在市場現有的各式各樣的多尺度建模框架中,Altair Multiscale Designer獨樹一格的將易用性、高效性、準確性和多功 能性進行了完美結合。
易用性
.......Multiscale Designer 提供了方便快捷的建立連續型、離散型複合材料定義及驗證的方法。用戶可定義單向加強型複合材料、編織型複合材料,可定義長短纖維加強,如光纖、玻鐵、凱夫拉加強的熱塑性、熱固性複合材料,整個過程可通過4個步驟快速實現:
- 2D和3D的繪圖環境輸出直角坐標、極座標、複數
- 線性材料屬性定義
- 模型降階
- 非線性材料屬性定義
.......建立的多尺度模型可通過虛擬實驗進行驗證,驗證後的材料模型,可耦合於Altair OptiStruct、Altair Radioss、LS-DYNA以及Abaqus,等知名的商業有限元素軟體,進行結構分析。
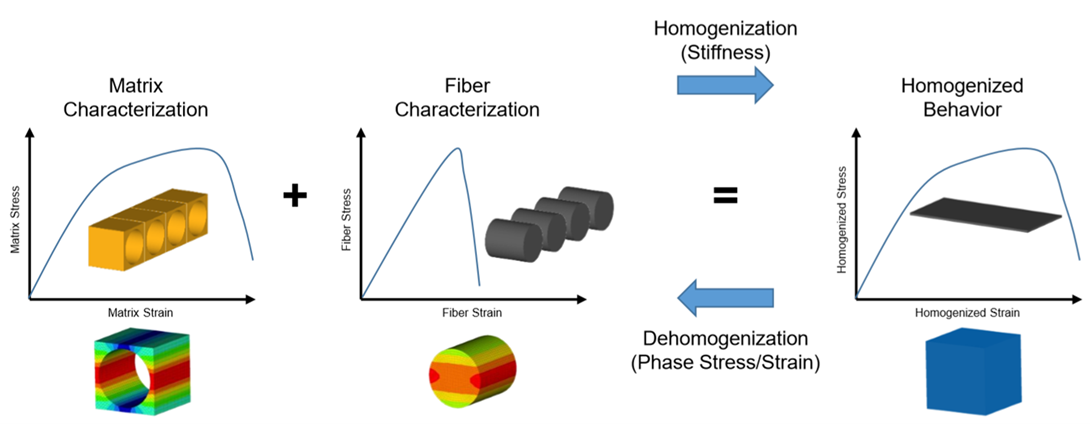
計算高效
.......傳統的針對多尺度材料分析的均勻化方法存在計算效率和計算精度無法同時滿足的問題, Multiscale Designer採用獨有的降階技術很好的解決了這個問題。Multiscale Designer先建立3D單胞模型,然後對單胞模型進行降階,通過對單胞模型進行一次計算得到單胞模型的宏觀各向異性線性和非線性材料參數,結合宏觀有限元素模擬時,每個元素的積分點會調用該材料參數進行剛性、應力的計算,無需重複求解單胞模型,很好的解決了計算效率及精度的問題。
高精度
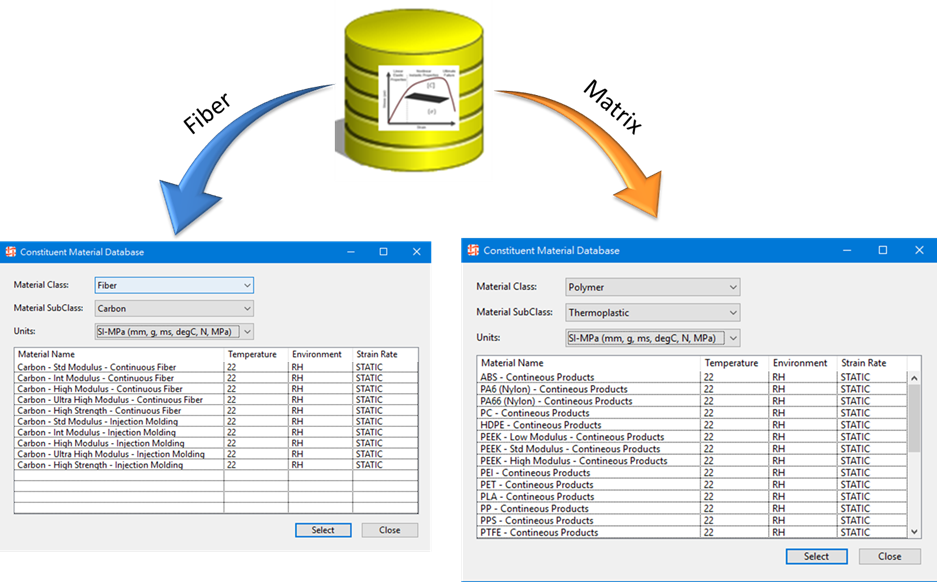
.......Multiscale Designer在單胞模型中為基體和纖維賦予了特有的非線性材料,這些模型包含針對脆性材料,如玻璃纖維、碳纖維的損傷模型,針對延性基體的塑性模型、高級混合損傷模型等。這些材料模型通過大量的實驗驗證了其在單向加強型複合材料、編織型複合材料和短切纖維增強複合材料上的準確性。
通用性
.......Multiscale Designer 內建了具備宏觀有限元素求解器,內部建立了參數化的標準試件庫,包括純剪、純彎、V型缺口試件及無缺口試件等,可快速對這些標準試件進行多尺度模擬。Multiscale Designer 隨機性分析模組集成了蒙特卡羅方法、稀疏網格隨機分析方法,每個材料參數 可通過均值、方差、機率分佈類型定義一個機率密度函數,隨機分析的輸出為機率密度函數,通過這些機率密度函數 可直接計算A、B許用值。

【 功能 】
力學特性分析與材料虛擬實驗室
.......Multiscale Designer - Mechanical基於微觀分析方法,直接對微觀介質進行線性和非線性的力學分析。獨一無二的基於特徵應變的單胞簡化模型使得多尺度分析的計算成本與傳統單一宏觀模型的計算成本相當。
.......Multiscale Designer - Mechanical提供正向和逆向建模功能。正向建模:輸入編織體構型、組分(纖維、基體)等工藝參數、力學性能參數,計算預測宏觀材料性能;逆向建模:輸入宏觀測試資料,部分組分性能,逆推組分性能,組合重現宏觀性能。其中逆向建模包括線彈性校核和非線性校核逆推。
.......Multiscale Designer - Mechanical針對50多種基準問題在各種複合材料產品形式的樣片和元件層級進行了驗證。
【 隨機性分析 】
.......Multiscale Designer-Stochastics提供正向和逆向隨機模擬功能。正向隨機模擬過程假定微觀幾何和構成屬性的可變性,由此計算出感興趣的宏觀數量的機率分佈函數。逆向隨機模擬過程根據宏觀(取樣片)層級實驗資料的可變性對微觀組成屬性的機率分佈函數進行分析。
Multiscale Designer-Stochastics 可直接提供獲得實驗資料支援的A、B 基準許用值。